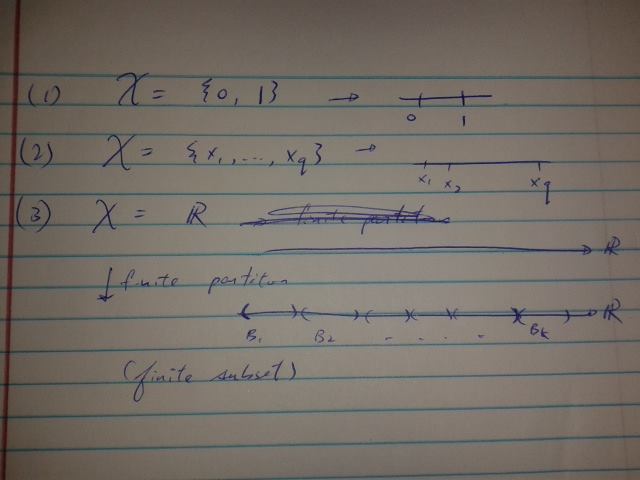29 Sep, 2015

Foundations for DP

Notes

Finite-dimensional vs. Infinite-dimensional Models

Dimensions Finite Infinite
Model Parametric BNP
Sample spcae $ \{ \theta = (\mu,\sigma) \} $ $\{ f(y;\theta): y \in \mathbb R \}$

Note that $\theta$ has infinite dimensions in the BNP model.

Model

  1. Parametric:
\[y_i = x_i'\beta + \epsilon_i, \epsilon_i \sim N(0,\sigma^2)\]
  1. Semi-parametric:
\[y_i | \beta,F \sim F(x_i'\beta),\]

where $x_i’\beta$ is the mean, median, etc.

  • $\beta \sim $ parametric prior
  • $F \sim $ prior for $F$ such that mean / median = $x_i’\beta$
  • So, one possibility: \(\begin{array}{rclcl} x_i'\beta &|& F &\sim& F \\\\ & & F &\sim& DP(F_0,\alpha) \\\\ \end{array}\)
  Parametric Classical nonparametric BNP
  $y_i = x_i’\beta + \epsilon_i$ No parametric assumptions Prior on $F$
    Only assumption: E[$\epsilon_i$] = 0  
    OLS, minimize $\sum(y_i-x_i’\beta)^2$  
    Get uncertainty using bootstrap, etc.  

Guassian Process (GP)

A Gaussian process is a statistical distribution $\mathbf X_t$, $t \in T$, for which any finite linear combination of samples has a joint Gaussian distribution. More accurately, any linear functional applied to the sample function Xt will give a normally distributed result. Notation-wise, one can write $X \sim \text{GP}(m,K)$, meaning the random function $\mathbf X$ is distributed as a GP with mean function $m$ and covariance function $K$. When the input vector $t$ is two- or multi-dimensional, a Gaussian process might be also known as a Gaussian random field.

Alternatively, a process[definition needed] is Gaussian if and only if for every finite set of indices $t_1,\ldots,t_k$ in the index set $T$ \({\mathbf{X}}_{t_1, \ldots, t_k} = (\mathbf{X}_{t_1}, \ldots, \mathbf{X}_{t_k})\) is a multivariate Gaussian random variable.

Study the Gaussian Process.

Foundations for the DP

Random distribution (like a random variable, but the distribution is a distribution) $Q$ on a sample space $\mathcal X$ (say $\mathcal X = \mathbb R$)

  1. $\mathcal X = \{0,1\}$
  2. $\mathcal X = \{x_1,x_2,…,x_q\}$
  3. $\mathcal X = \mathbb R$
    • Need a finite partition, subsets
    • sample space