13 Apr, 2016
Quiz 3 - Normal Distribution
Here’s an example question to help you prepare for quiz 3. You don’t have to write as much as I write here. I’m just writing out details to help you understand.
Quiz scores in AMS5 are distributed Normally. The average quiz score in AMS5 is 8. The standard deviation is .5. Find the percentage of students that scored over 8.5?
- Find the z-score: $z = \frac{8.5-8}{.5} = 1$
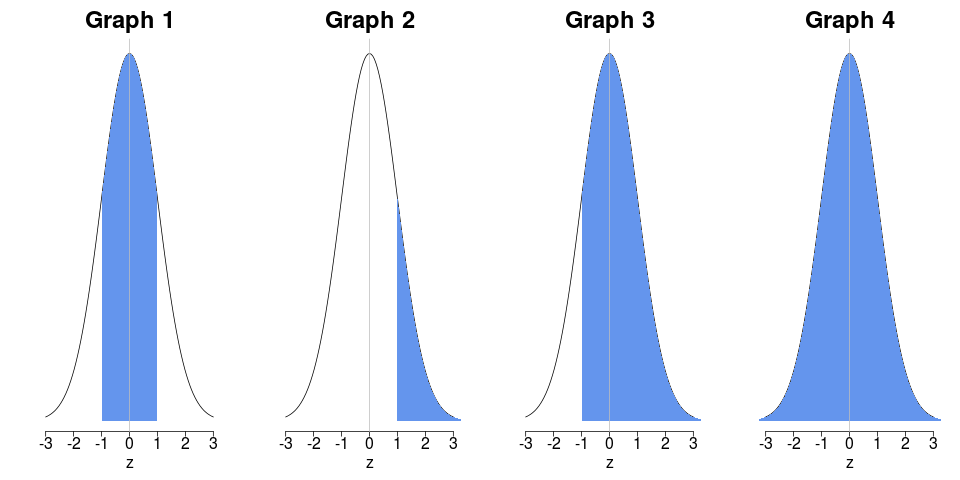
- Identify the shaded region of the standard normal distribution we are finding the area of.
- Convince yourself that the shaded area in Graph-2 corresponds to the percentage of students that scored over 8.5 (aka a z-score of 1).
- Since the table provided in your book only computes areas between a z-score and its negative, we can only compute (actually directly look up) the shaded area in Graph-1. Simply go to the table, look up a z-score of 1.00, and look across to find the area is 68.87%.
- Compute the shaded area. The area is the answer.
- Note that the Normal distribution is symmetric, and the total area under the curve (Graph-4) is 100%. So, the area in Graph-2 is simply $\frac{100\%-68.87\%}{2} = 15.565\% \approx 16\%$.
The following problem is a little different but very important as well.
Quiz scores in AMS5 are distributed Normally. The average quiz score in AMS5 is 8. The standard deviation is .5. Find the percentage of students that scored over 7.5?
- Find the z-score: $z = \frac{7.5-8}{.5} = -1$
- Identify the shaded region of the standard normal distribution we are finding the area of.
- Convince yourself that the shaded area in Graph-3 corresponds to the percentage of students that scored over 7.5 (aka a z-score of -1).
- Since the table provided in your book only computes areas between a z-score and its negative, we can only compute (actually directly look up) the shaded area in Graph-1. Simply go to the table, look up a z-score of 1.00, and look across to find the area is 68.87%.
- Compute the shaded area. The area is the answer.
- Note that the Normal distribution is symmetric, and the total area under the curve (Graph-4) is 100%. So, the area in Graph-3 is simply $\frac{50\%}{2}+\frac{68.87\%}{2} = 84.435\% \approx 84\%$.