8 Jan, 2016
Shrinkage & Regularization
OLS: Ordinary Least Square. $\hat{\beta} = \text{argmin}_\beta \norm{y-X\beta}^2 = (X’X)^{-1}X’y$
Ridge Regression:
- minimize $\norm{y-X\beta}^2$ s.t. $\norm{\beta}^2 \lt s$
- minimize $(y-X\beta)^2 + \lambda\sum \beta_j^2$
- $\tilde{\beta} = (X’X+\lambda I)^{-1}X’y$
library(MASS)lm.ridge(y~X, lambda=lambda_vector)- Choose $\lambda$ using cross validation (based on $\text{MSE}_k = \sum (y_i-\hat{y}_i)^2$)
- MSE = $\sum \text{MSE_k} / K$
- k-fold if $n$ is large
- leave one out if $n$ is small
- choose $\lambda$ that minimizes MSE
- Note that we don’t penalize the intercept, because it’s the coefficient for predictors.
- Typical to standardize to make scale invariant
- Disadvantage: coefficients are shrunk to zero, but not exactly zero. So, coefficients tend to be smaller than the truth, but the model doesn’t select variables.
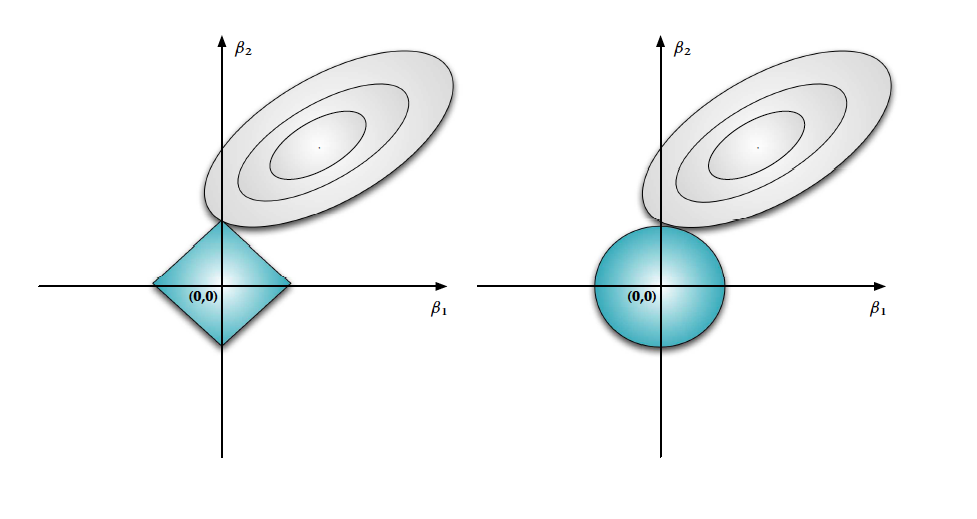
Lasso:
- uses $l_1$ penalty instead of $l_2$
-
$\newcommand{\norm}[1]{\left\lVert#1\right\rVert} \norm{y-X\beta}_2 = \frac{(\beta-\hat\beta)X’X(\beta-\hat\beta)}{\norm{y’(I-P_x)y}}$, where $P_x$ is the projection matrix. This is the form of an ellipse.